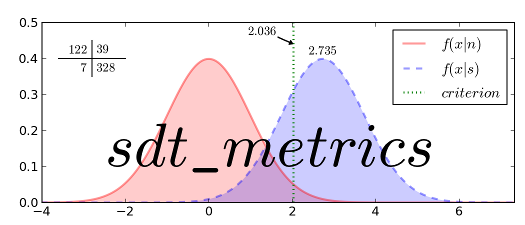

Signal Detection Theory (SDT) has come to be an invaluable tool to psychology and other disciplines. The underlying theory suggests that a discriminator (albeit a human, machine classifier, or diagnostic test) detects the presence of a signal buried in noise. The performance of the discriminator is assessed in terms of sensitivity and response bias. Sensitivity describes how well the signal + noise distribution is segregated from the noise distribution. Response bias or decision bias describes systematic over-or-underestimates the probability of a true event.
This package provides a collection of metrics for assessing signal detection performance.
View the Installation Instructions
Let’s cut to the chase
>>> from __future__ import division
>>> from sdt_metrics import dprime
>>> hi,mi,cr,fa = 121,42,56,34
>>> dprime(hi,mi,cr,fa)
0.9618717480344676
If given two arguments it’ll treat them as probabilities
>>> phi = hi/(hi+mi)
>>> pfa = fa/(cr+fa)
>>> dprime(phi, pfa)
0.9618717480344676
Functions also take list-like data
>>> dprime([.5, .6, .7],
[.5, .5, .5])
[0.0, 0.2533471028599986, 0.5244005132792952]
sdt_metrics.SDT is a collections.Counter-like object for storing data
>>> from sdt_metrics import HI,MI,CR,FA, SDT
>>> sdt_obj = SDT(HI=73,FA=32)
>>> print(sdt_obj)
SDT(HI=73, MI=0, CR=0, FA=32)
>>>
>>> sdt_obj(MI) # add a miss
>>> print(sdt_obj)
SDT(HI=73, MI=1, CR=0, FA=32)
>>>
>>> sdt_obj[CR]+=5 # add 5 correct rejections
>>> print(sdt_obj)
SDT(HI=73, MI=1, CR=5, FA=32)
>>>
>>> sdt_obj.aprime() # metrics are methods of SDT
0.7558219178082192
| dprime | d’ |
| loglinear_dprime | loglinear d’ |
| beta | beta |
| c | c |
| loglinear_beta | loglinear beta |
| loglinear_c | loglinear c |
| poc_plot | Probability of Occurence Curves (POC) Plot |
| roc_plot | Receiver Operating Characteristics (ROC) Plot |
| mult_roc_plot | Multiple ROC Curves Plot |
| metric_validation_plot | pcolor plot of the metric over ROC space |
| Sensitivity Scatter Matrix | Scatter Matrix comparing dprime, aprime, amzs, accuracy |
| Probability Scatter Matrix | Scatter Matrix comparing mcc, f1, mutual_info, accuracy |
| Bias Scatter Matrix | Scatter Matrix comparing log(beta), c, bppd, loglinear_bppd, log(bmz) |
| Analysis of loglinear_bppd | Addresses boundary sensitivity problems of bppd |