dprime¶

Download [hi-res] [pdf]

class sdt_metrics.dprime(methodname, add_prob_method=False)¶

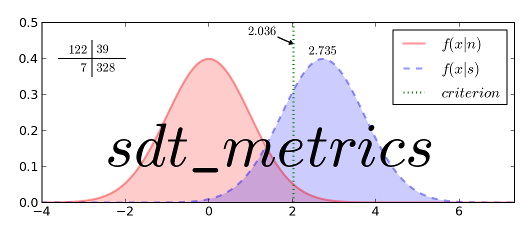
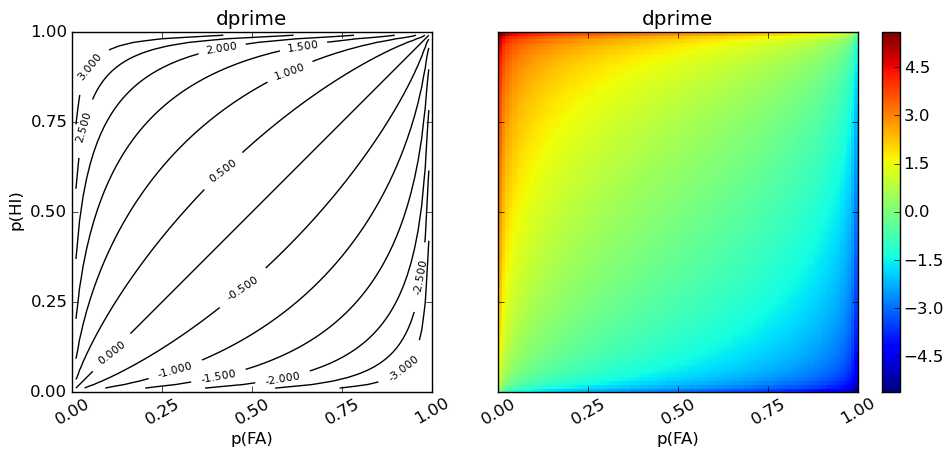
d’: parametric measure of sensitivity

Extremely popular measure adapted by from communication engineering by psychologists in the 1950s [1]. Most notable text is Green and Swets [2]. Calculation uses the formula given by Macmillan [3]. Extreme probabilities of 0 and 1 are treated using the correction suggested by Macmillan and Kaplan [4]. Rates of 0 are replaced with 1/(2n) and rates of 1 are replaced wtih 1 - 1/(2n). This approach has been shown to be biased (Miller [5]). Hautus’s [6] loglinear approach may be preferred. For a more extensive overview on treating extreme values see Stanislaw and Todorov [7].

See also

loglinear_dprime()

[1]	Szalma, J. L., and Hancock, P. A. Signal detection theory. Class Lecture Notes. http://bit.ly/KIyKkt

[2]	Green, D. M., and Swets J. A. (1996/1988). Signal Detection theory and psychophysics, reprint edition. Los Altos, CA: Penisula Publishing.

[3]	Macmillan, N. A. (1993). Signal detection theory as data analysis method and psychological decision model. In G. Keren & C. Lewis (Eds.), A handbook for data analysis in the behavioral sciences: Methodological issues (pp. 21-57). Hillsdale, NJ: Erlbaum.

[4]	Macmillan, N. A., and Kaplan, H. L. (1985). Detection theory analysis of group data: Estimating sensitivity from average hit and false-alarm rates. Psychological Bulletin, 98, 185-199.

[5]	Miller, J. (1996). The sampling distribution of d’. Perception and Psychophysics, 58, 65-72.

[6]	Hautus, M. (1995). Corrections for extreme proportions and their biasing effects on estimated values of d’. Behavior Research Methods, Instruments, and Computers, 27, 46-51.

[7]	Stanislaw H. and Todorov N. (1999). Calculation of signal detection theory measures. Behavorial Research Methods, Instruments, and Computers, 31 (1), 137-149.

classmethod direct(*args)¶

Calculates metric based on hit, miss, correct rejection, and false alarm counts

static prob(*args)¶

Calculates metric based on hit rate and false alarm rate

classmethod __call__(*args)¶

based on the number of args and the availability of .prob routes call to appropriate method.